Determining whether a file or directory exists is crucial for conditional execution and error handling in Bash scripting. This capability aids users in decision-making when using scripts and ensures a smooth command execution.
This process avoids errors and unexpected script behavior by validating the existence of necessary resources before proceeding further.
In this guide, learn how to use a bash command to check if a file or directory exists.

Prerequisites
- A Linux operating system.
- Access to a terminal window / command line (Ctrl+Alt+T).
Note: A bash script is a sequence of several commands to the shell. It can be saved as a file and is often used to automate multiple system commands into a single action.
Check if a File Exists in Bash
Conditional statements and specific commands like test or [ ] allow users to verify the presence of a file on the system. The test command accepts many options, allowing it to find specific file types.
Some of the options are:
| Option | File Type |
|---|---|
-f | file |
-d | directory |
-L | symbolic link |
-r | readable |
-x | executable |
-w | writable |
For example, to test if the file /tmp/test.log exists, run the following command:
test -f /tmp/test.txtThe first line executes the test to see if the file exists. The second command, echo, displays the results. The result 0 means that the file exists, while 1 means no file was found.
echo $?In our example, the result was 1:

Now try creating a file with touch, and then perform a test:
touch /tmp/test.txttest -f /tmp/test.txtecho $?As we have created the file beforehand, the result now is 0:

You can also use square brackets instead of the test command:
[ -f /tmp/test.txt ]echo $?
Check if a File Does not Exist
Testing for a file returns 0 (true) if the file exists and 1 (false) if it does not exist. For some operations, you may want to reverse the logic. It is helpful to write a script to create a particular file only if it doesn’t already exist.
To do so, enter the following command:
[ ! -f /tmp/test.txt ] && touch /tmp/test.txtThe exclamation point ! stands for not. This command ensures there is no file named test.txt in the /tmp directory and then creates the file.
To see if the system created the file, run the following:
ls /tmp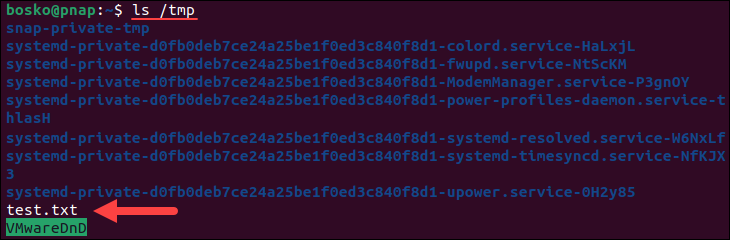
You should see test.txt listed in the command output. Use a similar command to look for a directory and replace the -f option with -d:
[ ! -d /tmp/test ] && touch /tmp/test Check if a Directory Exists in Bash
To check if a directory exists, switch the -f option on the test command with -d (for directory). For example:
test -d /tmp/testecho $?
The output is 1, which means that the directory doesn't exist. Create the directory using the mkdir command and rerun the test:
mkdir /tmp/testtest -d /tmp/testecho $?
The command output is 0, which means that the directory exists. The test command works the same as it does for files, so using brackets instead of the test command works here too.
Note: If you are searching for a file or directory because you need to delete it, refer to our guide on removing files and directories with Linux command line.
Check if a File or Directory Exists Using Code Snippets
The previous commands work well for a simple two-line command at a command prompt. However, you can also use Bash with multiple commands. When several commands are strung together, they are called a script.
A script is usually saved as a file and executed. Scripting also uses logical operators to test for a condition and then takes action based on the test results.
Check for File or Directory
Follow the steps below to check if a file or directory exists:
1. Create a script file using a text editor such as nano:
nano bashtest.sh2. Enter one of the snippets from below and make sure to include the #!/bin/bash shebang.
The following code snippet tests for the presence of a particular file. If the file exists, the script displays File exists on the screen.
#!/bin/bash
if [ -f /tmp/test.txt ]
then
echo "File exists"
fiIf you’re checking for a directory, replace the -f option with -d:
#!/bin/bash
if [ -d /tmp/test ]
then
echo "The directory exists"
fiThis script checks for the directory /tmp/test. If it exists, the system displays The directory exists.
3. Use Ctrl-o to save the file, then Ctrl-x to exit. Then, run the script by entering:
bash bashtest.shUsing Code Snippets to Check for Multiple Files
It is also possible to check if multiple files exist using the if conditional statements. Follow the steps below to create a script and verify the existence of multiple files simultaneously:
1. Create a new Bash script using your preferred text editor:
nano script.sh2. Paste the following code and replace <file1> and <file2> with the full path to the files you want to check:
#!/bin/bash
if [[ -f <file1> ]] && [[ -f <file2> ]]
then
echo "The files exist!"
fiSave and exit the script file.
3. Run the script:
bash script.sh
Change the -f option to -d to run the same test for multiple directories.
Conclusion
You can now use bash to check if a file and directory exist. You can also create simple test scripts as you now understand the functions of a basic bash script file.
Next, check out our post on Bash Function.



