Quadrature amplitude modulation (QAM) is a sophisticated modulation technique used widely in modern communication systems, particularly in digital communications. QAM combines two modulation schemes—amplitude modulation (AM) and phase modulation (PM)—to transmit data over various media, including wireless and wired networks.
What Is Quadrature Amplitude Modulation?
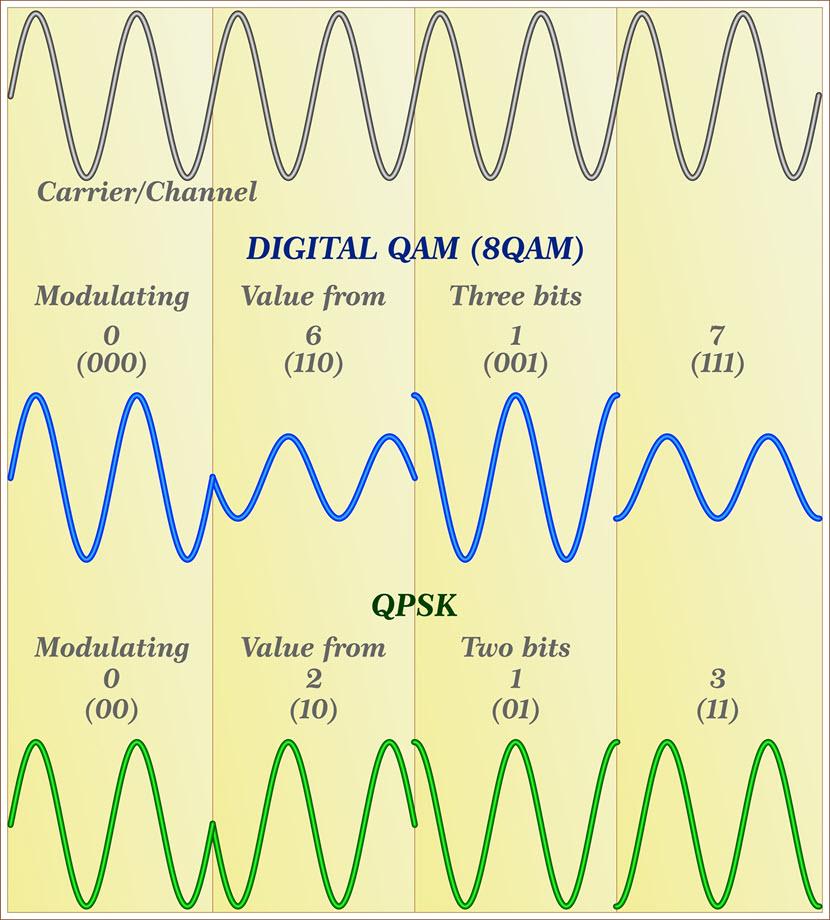
Quadrature amplitude modulation (QAM) is a technique that encodes information into a carrier signal by altering its amplitude and phase. The modulation process involves creating two orthogonal components of the carrier signal, known as the in-phase (I) and quadrature (Q) components, which are 90 degrees out of phase with each other. These components are modulated independently with separate data streams, and the resulting modulated signals are combined to form the final QAM signal. The combination of these components allows QAM to represent a wide range of amplitude and phase states, each corresponding to a unique symbol in a constellation diagram.
The constellation diagram is a key concept in understanding QAM. It is a graphical representation where each point, or constellation point, corresponds to a specific amplitude and phase combination, encoding a unique symbol. The number of points in the constellation diagram determines the order of QAM (e.g., 16-QAM, 64-QAM, 256-QAM), with higher-order QAM schemes representing more bits per symbol. For instance, 16-QAM uses 16 constellation points, each representing a 4-bit symbol, while 256-QAM uses 256 points, representing 8-bit symbols. This ability to encode multiple bits per symbol gives QAM high spectral efficiency.
QAM can be implemented in both analog and digital systems. However, digital QAM is more commonly used today due to its superior noise resilience and ability to support higher data rates. In digital communication systems, QAM plays a vital role in modulating signals for transmission over various media, including coaxial cables, fiber optics, and wireless channels.
How Does QAM Work?
The operation of QAM involves several technical steps that ensure efficient and reliable data transmission. Here is a detailed examination of these steps:
Carrier Signal Generation
The process begins with the generation of a carrier signal, typically a sinusoidal waveform at a specific frequency. This carrier signal is then split into the in-phase (I) component and the quadrature (Q) component. These components are orthogonal, meaning they are phase-shifted by 90 degrees relative to each other, allowing independent modulation.
Data Stream Division and Mapping
The input data stream is divided into two parallel streams, which are then mapped onto symbols based on the desired QAM order. This mapping involves assigning a specific amplitude and phase combination to each symbol, corresponding to a point in the constellation diagram. The bit sequence is grouped according to the number of bits each symbol represents. For instance, in 64-QAM, the bit sequence is divided into 6-bit groups, with each group mapped to one of the 64 constellation points.
Modulation of I and Q Components
Each data stream modulates the amplitude of the corresponding I or Q component. The modulation process involves adjusting the amplitude of the carrier signal according to the mapped symbols. The I component modulates the in-phase carrier, while the Q component modulates the quadrature carrier. The result is two amplitude-modulated signals, each representing a distinct aspect of the original data stream.
Combining I and Q Signals
The modulated I (in-phase) and Q (quadrature) signals are combined to create the final QAM signal. This combination involves summing the two components, resulting in a single composite signal. The combined signal varies in amplitude and phase, reflecting the contributions from the I and Q components. This composite signal is then transmitted, carrying the encoded information through its varying amplitude and phase characteristics. Combining these two orthogonal signals allows QAM to efficiently convey data over a communication channel.
Transmission and Reception
The composite QAM signal is transmitted over the communication channel. At the receiver end, the signal is demodulated by separating it into its I and Q components using coherent detection, which involves mixing the received signal with local oscillators synchronized with the carrier frequency. The demodulated I and Q signals are then mapped back to their respective symbols using the constellation diagram.
Error Correction and Decoding
In digital QAM systems, error correction techniques such as forward error correction (FEC) are applied to mitigate the effects of noise and interference. After error correction, the symbols are decoded back into the original data stream. The performance of QAM in terms of bit error rate (BER) is highly dependent on the signal-to-noise ratio (SNR) and the order of the QAM scheme used.
Higher-order QAM, such as 64-QAM or 256-QAM, increases the number of bits transmitted per symbol, enhancing data throughput. However, these higher-order schemes also require a higher SNR to accurately distinguish between closely spaced constellation points, making them more susceptible to noise and distortion.
Why Is QAM Important?
QAM is a cornerstone of modern digital communication systems due to the factors listed below.
- Spectral efficiency. QAM provides high spectral efficiency by transmitting multiple bits per symbol. This efficiency is particularly important in bandwidth-limited systems, where maximizing data transmission within the available spectrum is crucial. Encoding more bits per symbol allows QAM to achieve higher data rates than simpler modulation schemes like binary phase shift keying (BPSK) or quadrature phase shift keying (QPSK).
- High data rates. The ability of QAM to support high data rates makes it indispensable in applications requiring fast data transfer, such as video streaming, online gaming, and broadband internet. Higher-order QAM schemes, such as 256-QAM, enable the efficient transmission of large amounts of data, making them ideal for modern high-bandwidth applications.
- Adaptability to channel conditions. QAM's flexibility allows it to be adapted to various channel conditions. For example, higher-order QAM (like 256-QAM) can be used in high-quality channels with low noise levels to maximize data throughput. Conversely, lower-order QAM (like 16-QAM) can be employed in noisier environments to maintain reliable communication. This adaptability is particularly useful in mobile networks, where signal conditions vary significantly.
- Wide application range. QAM is used across a diverse array of communication systems, from digital television and broadband internet to satellite communications and wireless networks. Its ability to efficiently handle analog and digital signals makes it a versatile choice for many types of data transmission.
- Advanced modulation techniques. QAM serves as a foundation for more advanced modulation techniques, such as orthogonal frequency division multiplexing (OFDM), which is used in technologies like LTE, Wi-Fi, and DVB-T. QAM is employed on multiple subcarriers in these systems to increase the overall data rate and spectral efficiency.
Advantages and Disadvantages of QAM
Quadrature amplitude modulation offers significant benefits but also presents certain challenges.
QAM Advantages
Here are the benefits of QAM:
- Increased data rates. QAM's ability to encode multiple bits per symbol enables higher data rates compared to simpler modulation schemes. This is particularly important in applications that demand rapid data transfer, such as broadband internet and high-definition video streaming.
- Efficient bandwidth utilization. By modulating both amplitude and phase, QAM optimizes available bandwidth. This is critical in environments with limited bandwidth, such as in wireless networks, allowing more data to be transmitted within the same spectral space.
- Scalability. QAM can be easily scaled to higher orders (e.g., 64-QAM, 256-QAM) to increase data throughput. This scalability allows communication systems to adapt to varying channel conditions by selecting the appropriate modulation level. Higher-order QAM schemes can maximize data rates in good channel conditions, while lower-order schemes ensure reliability in more challenging environments.
- Compatibility with multiple systems. QAM's compatibility with digital and analog systems enhances its versatility across different communication platforms and makes it suitable for various applications, from traditional broadcast media to cutting-edge digital communication technologies.
QAM Disadvantages
Here are the drawbacks of QAM:
- Susceptibility to noise and interference. Higher-order QAM schemes are more susceptible to noise and interference due to the closer spacing of constellation points. This sensitivity can lead to higher error rates, especially in environments with poor signal quality or high interference levels.
- Complexity in implementation. Implementing QAM, particularly higher-order schemes, requires sophisticated signal processing techniques and precise synchronization between the transmitter and receiver. This complexity increases communication devices' cost, power consumption, and design challenges.
- Higher power requirements. A higher signal-to-noise ratio (SNR) is necessary to maintain signal integrity in higher-order QAM. This often translates into higher power consumption, which can be a drawback in portable and battery-operated devices where energy efficiency is critical.
- Limited range for higher-order QAM. As the order of QAM increases, the effective transmission range tends to decrease due to greater susceptibility to attenuation and distortion over distance. This